Arctic Fuzz 1M reverse log

[roccster]

Hi all,

I have a q about the Arctic Fuzz (http://tagboardeffects.blogspot.se/2013/08/bjfe-arctic-white-fuzz.html) the layout suggests a 1M reverse log pot for the Fuzz, but that seems a bit hard to get hold of here. Is there a decent substitute? I just mannaged to get hold of a 1M lin pot, but don´t know if that will work.

Cheers!


/ Richard

[induction]

The circuit will work with any taper. The question is only how well you like the sweep. I'd try a linear and see if you are dissatisfied. Since it's a variable resistor, if you have a bigger value linear pot, you can use a bridging resistor to alter the taper for more reverse log behavior. See the bottom of this page.

[roccster]

Wow, super fast reply, I like that :D

Thanx m8, I will check that out.

rgds
/ Richard

[roccster]

Ok, i dont relly follow the naming of the lugs, ccw etc... Can you give me a hint between which lugs (1, 2, 3) the resistor goes, and what value to use?

Cheers!


/ Richard

[Ciaran Haslett]

Following the convention used here...

CCW = 1
CW = 3

So the resistor in the linked geofex page goes between Lugs 1 and 2

The graph displays the kind of sweep you'll get depending on the size of the resistor used (as a fraction of the total pot resistance).  So pick your fraction and try it out.  If you have a breadboard handy you could very quickly test different values without soldering and find the sweep you prefer.

Ciaran

[induction]

Sorry. I should have done more homework on this before responding. The bridging resistor trick won't work here. It only works on for variable resistors that increase resistance as you turn up the pot. (See details below, if you are interested in the math.) These are wired between lugs 1 (aka CCW) and 2.  In this case, the pot is a variable resistor wired to decrease resistance as you turn up the pot (ie. wired between lugs 2 and 3 (aka CW)). It adds series resistance to the input signal to reduce the fuzz as you turn down the pot. I would suggest trying the linear pot you have and see how well it works for you. If you don't like it, you have to decide what you don't like about it: the range or the sweep. That is, how much of that 1M is usable (range) and how smoothly does the sound change as you dial it (sweep)? Find the minimum and maximum settings you will use, and report back if you don't know what to do next.

Alternately you could use a 1M log taper pot wired between lugs 1 and 2. That would fix the sweep, but the rotation would be backwards.

For posterity, here's a quick summary of the bridging resistor method: If you need an antilog pot that will be wired as a variable resistor between lugs 1 and 2 (increasing the resistance as you dial up the pot). You can take a linear pot of a higher value and put a resistor across lugs 1 and 2 to give you an approximation of an antilog taper. The resistor should be the value that gives an equivalent maximum resistance when put in parallel with the pot that you use.

To figure out the values of the new pot and resistor, we need to do some math. Resistors in parallel give an equivalent resistance of Rp = R1*R2/(R1+R2). We know Rp (it's the value of the pot you want to  replace), and we want to find R1 (the new pot) and R2 (the bridging resistor). Mathematically, this is one equation with two unknowns, so there are infinitely many combinations of R1 and R2 that will work. In practice, we are limited by the pots. Resistors can be found in almost any value you want, but pots only come in so many values. We can rearrange the equivalent resistance equation like this: R1 = Rp*(b+1), where b is R1/R2. Values of b that give a good antilog sweep range from 2 to 5 (the larger b is, the more deviation from linearity the resulting pot will have). So choose b = 3, plug it in to the equation and find R1 (4M, in this case). Then adjust b up or down until you find a value of R1 that represents a linear pot you can get your hands on. Then find R2 = R1/b. Attach R2 between lugs 1 and 2 of R1, and presto.

With an antilog pot, the resistance between lugs 1 and 2 starts at 0, increases quickly at low settings, increases slowly at higher settings and ends up at the value of the pot: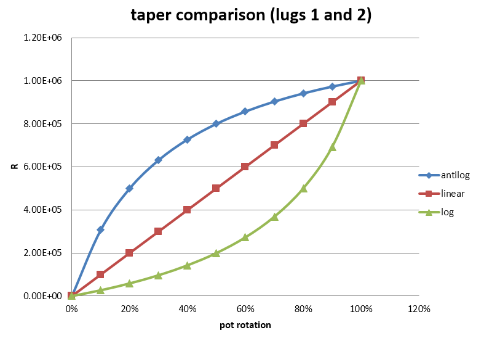



Thus the resistance between lugs 2 and 3 starts at the value of the pot at high settings, decreases quickly at low settings, decreases slowly at higher settings, and ends up at 0. This is the behavior you want from your replacement pot. You might try putting the resistor between lugs 2 and 3, but the math doesn't work out. Instead of a decreasing antilog response you get a decreasing log response.



There are no tricks that I am aware of that will give a decreasing antilog response from a linear resistor, but maybe they just haven't been discovered yet. Until then, I'd try the linear pot and see how it works.